Question

Triangle ABC is dilated by a scale factor of 0.5 with the origin as the center of dilation, resulting in the image triangle A'B'C'. If A=(2,2), b=(4,3), and C=(6,3), what is the length of bar (B'C')

Answer 1

Length of BC = sqrt( (6-4)^2 + (3-3)^2) = sqrt 4 = 2

So as the factor of dilation is 0.5 the length of B'C' = 0.5*2 = 1 (answer)

Answer 2

Answer: 1 units

Explanation:

Given : Triangle ABC is dilated with the origin as the center of dilation, resulting in the image triangle A'B'C'.

The scale factor dilation (k) = 0.5

To find the length of
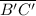`\overline{B'C'}` , first we need to calculate the distance from B to C or
`\overline{BC}`

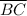
If B=(4,3), and C=(6,3), then , by using distance formula

`BC=√((3-3)^2+(6-4)^2)=√(0^2+2^2)=√(4)=2`

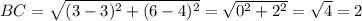
Now, the length of B'C' =
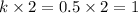`k*2=0.5*2=1` units

Hence, the length of B'C' = 1 units