Answer:
x + 2x - 3 = 26
Explanation:
Define the variables:
- Let x = length of Nate's car.
- Let y = length of Maya's car.
If Maya's car is 3 inches less than 2 times the length of Nate's car, then:
⇒ y = 2x - 3
If the sum of the lengths of both cars is 26 inches, then:
⇒ x + y = 26
Substitute the found expression for y into the equation:
⇒ x + y = 26
⇒ x + (2x - 3) = 26
⇒ x + 2x - 3 = 26
Therefore, the equation to determine the lengths of Nate'a and Maya's cars is:
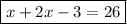
Solving the equation for x
⇒ x + 2x - 3 = 26
⇒ 3x - 3 = 26
⇒ 3x - 3 + 3 = 26 + 3
⇒ 3x = 29
⇒ 3x ÷ 3 = 29 ÷ 3
⇒ x = 9.7 in (nearest tenth)
Therefore, Nate's car is 9.7 in (nearest tenth).
To find the length of Maya's car, subtract the length of Nate's car from 26:
⇒ 26 - 9.7 = 16.3 in (nearest tenth).
Therefore, Maya's car is 16.3 in (nearest tenth).