Answer: The correct option is (D)
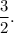
Step-by-step explanation: Given that rectangle M was dilated to form rectangle M'.
We are to select the ratio that is the scale factor of dilation.
We know that
the scale factor of dilation is defined as follows :
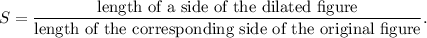
In the given dilation, we have
length of a side of the original rectangle = 4 units
and
the length of the corresponding side of the dilated rectangle = 6 units.
Therefore, the required scale factor of dilation is given by
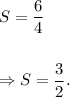
Thus, option (D) is CORRECT.