Let r be the radius
Area of the shaded part (which is 2 complete circles)
= 2 x πr²
= 2πr²
Area of the unshaded part (which is a square that has a length 2r)
= 2r x 2r
= 4r²
Probability that the point is in the unshaded area
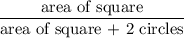

Answer: 0.4 (nearest tenth)