Question

The given function represents the position of a particle traveling along a horizontal line. s(t) = 2t3 − 3t2 − 36t + 6 for t ≥ 0 (a) find the velocity and acceleration functions.

Answer 1

1) The velocity of the particle is given by the derivative of the position. So, if we derive s(t), we get the velocity of the particle as a function of the time:

`v(t)=s'(t)=(2t^3-3t^2-36t+6)'=6t^2-6t-36`

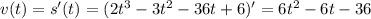
2) The acceleration of the particle is given by the derivative of the velocity. So, if we derive v(t), we get the acceleration of the particle as a function of the time:

`a(t)=v'(t)=(6t^2-6t-36)'=12t-6`