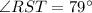Question

What is the measure of RST?

Answer 1

Answer: the correct answer is B (apex)

Answer 2

Answer: B.
`79^(\circ)`

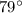
Explanation:

In the given picture, we have a circle with the measure of arc RT=
`158^(\circ)`

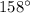
Let the center of the given circle be O.

Since, the angle subtended by an arc at the center =measure of arc

Therefore, the angle subtended by an arc RT at the center =
`\angle{ROT}=158^(\circ)`

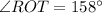
Also, the angle which is subtended by an arc at the center of a circle is double the size of the angle subtended at any point on the circumference.

i.e.
`\angle{ROT}=2\angle{RST}`

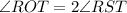
Thus, the measure of
`\angle{RST}=\frac{\angle{ROT}}{2}=(158^(\circ))/(2)=79^(\circ)`

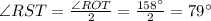
Hence, the measure of
`\angle{RST}=79^(\circ)`