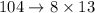Question

An army contingent of 104 members is to march behind an army band of 96 members in a parade.

Answer 1

You can dispose a number
`x` of elements in a matrix-like formation with
`n* m` shape if and only if
`n` and
`m` both divide
`x`, and also
`nm=x`.

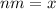So, we need to find the greatest common divisor between
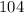`104` and
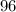`96`, so that we can use that divisor as the number of columns, and then.

To do so, we need to find the prime factorization of the two numbers:

`104 = 2^3* 13`

`96 = 2^5 * 3`

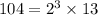
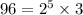
So, the two numbers share only one prime in their factorization, namely
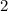`2`, but we can't take "too many" of them:
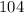`104` has "three two's" inside, while
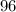`96` has "five two's" inside. So, we can take at most "three two's" to make sure that it is a common divisor. As for the other primes, we can't include
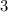`3` nor
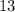`13`, because it's not a shared prime.

So, the greater number of columns is
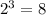`2^3=8`, which yield the following formations:

`104 \to 8* 13`

`96 \to 8* 12`