Question

I’m confused on this one

Answer 1

To find AC we need to find EC. We do this by using the Pythagorean Theorem to find a side with one side 7 and the hypotenuse root 130:

`{a}^(2) = {b}^(2) + {c}^(2) \\ {c}^(2) = {a}^(2) - {b}^(2) \\ c = \sqrt{ {a}^(2) - {b}^(2) } \\ c = \sqrt{ {( √(130) )}^(2) - {(7)}^(2) }`

`c = √(130 - 49) \\ c = √(81) \\ c = 9`

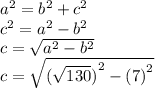
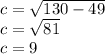
First, we single out the variable we want (C). Then, we plug in the numbers. We find that length EC is 9 inches. Therefore, AC is 24 + 9 = 33 inches.

To find AD, we must use the Pythagorean Theorem. Since this shape is symmetrical, we know that EB = ED, so ED = 7 in. Now we just need to find the hypotenuse:

`a = \sqrt{ {b}^(2) + {c}^(2) } \\ a = \sqrt{ {(7)}^(2) + {(24)}^(2) } \\ a = √(49 + 576) \\ a = √(625) = 25`
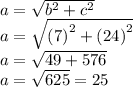
First, we plug in the legs of the triangle, and then simplify. Therefore, the length AD is 25 inches.

Since this shape is a kite, ED and EB are congruent. Therefore, ED is 7 inches.