Question

I'm reasking a previous question to make it more clear. This is a Linear Equation that I must solve. It includes fractions (the 2 terms on the left side). Here goes: x÷2 - (10x-25)÷10 = 3(x+3) - (x-14). Please help

Answer 1

x/2 - (10x - 25)/10 = 3(x + 3) - (x - 14)

Multiply each term by 10 to eliminate the fractions:-

5x - (10x - 25) = 30(x + 3) - 10(x - 14)

5x - 10x + 25 = 30x + 90 - 10x + 140

5x - 10x - 30x + 10x = 90 + 140 - 25

-25x = 205

x = -8.2 answer

Answer 2

Assuming the equation is:

`(x)/(2)-(10x-25)/(10)=3(x+3)-(x-14)`

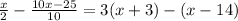
When fractions involve numeric denominators, the fractions can be removed by multiplying (both sides) by the LCM of the denominators.

Here the denominators are 2 and 10, hence the LCM is 10.

Multiply by 10 on both sides, not forgetting to distribute when multiplying on the right side:

`10(x)/(2)-10(10x-25)/(10)=10*3(x+3)-10(x-14)`

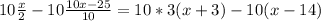
simplify, remember that there are always implied parentheses around numerators and denominators:

`5x-(10x-25)=30(x+3)-10(x-14)`

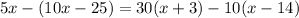
Now, distribute, i.e. remove parentheses and distribute:

5x-10x+25=30x+90-10x+140

Simplify

-5x+25=20x+230

transpose terms

25-230=20x+5x

solve

x=-205/25=-41/5

In this particular case, we can also take advantage of the term

(10x-25)/10=5(2x-5)/10=(2x-5)/2 which greatly simplifies the solution process, because the LCM will then be 2 instead of 10.

If we do that, the solution will be:

Multiply by 2 on both sides, not forgetting to distribute when multiplying on the right side:

`(x)/(2)-(10x-25)/(10)=3(x+3)-(x-14)`

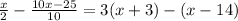
simplify, remember that there are always implied parentheses around numerators and denominators:

`2(x)/(2)-2(2x-5)/(2)=2*3(x+3)-2(x-14)`

`x-(2x-5)=6(x+3)-2(x-14)`

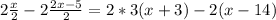
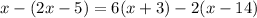
Now, distribute, i.e. remove parentheses and distribute:

`x-2x+5=6x+18-2x+28`

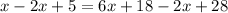
Simplify

-x+5=4x+46

solve

5-46=4x+x

-41=5x

x=-41/5

with the same results.