Question

in what distance can a 1500kg automobile be stopped if the brake is applied when the speed is 20m/s and the coefficient of sliding friction is 0.7 between the tyres and the ground?please I need a full step by step explanation

Answer 1

1) The braking force is provided by the frictional force, which is given by:

`F_f=\mu m g`

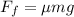
where

`\mu=0.7` is the coefficient of friction

m=1500 kg is the mass of the car

`g=9.81 m/s^2` is the gravitational acceleration

Substituting numbers into the equation, we find

`F_f= (0.7)(1500 kg)(9.81 m/s^2)=10301 N`

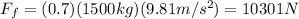
2) The work done by the frictional force to stop the car is equal to the product between the force and the distance d:

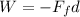`W=-F_fd` (1)

where we put a negative sign because the force is in the opposite direction of the motion of the car.

3) For the work-energy theorem, the work done by the frictional force is equal to the variation of kinetic energy of the car:

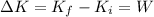`\Delta K=K_f -K_i =W` (2)

The final kinetic energy is zero, so the variation of kinetic energy is just equal to the initial kinetic energy of the car:

`\Delta K=-K_i=-(1)/(2)mv^2=-(1)/(2)(1500 kg)(20 m/s)^2=-300000 J`

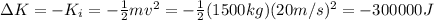
4) By equalizing eq. (1) and (2), we find the distance, d:

`-K_i = -Fd`

`d=(K_i)/(F)=(300000 J)/(10301 N)=29.1 m`