ANSWER
The correct answer is option D.
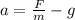
EXPLANATION
The given formula is
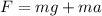
We want to solve this formula for a, so we add
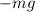
to both sides of the equation to get,
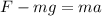
We now divide through by m, to obtain,
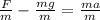
Let us cancel out the common factors to get,
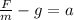
We can also rewrite this to obtain,
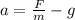
Therefore the correct answer is D.