The standard form of sine and cosine functions are given by these equations:
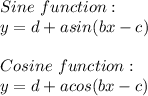
So let's compare each topic as follows:
1. Period
The period
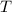 of these two functions is the same. So, let
of these two functions is the same. So, let
 be a positive real number. The period of
be a positive real number. The period of
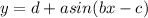 and
and
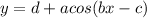 is given by:
is given by:
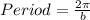
2. Shape
If you want to graph the sine function, you need to mark the angle along the horizontal
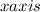 , and for each angle, you put the sine of that angle on the vertical
, and for each angle, you put the sine of that angle on the vertical
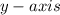 . As a result, a smooth curve that varies from +1 to -1 is formed as indicated in the blue curve below. We call this type of curves sinusoidal after the name of the sine function. This shape is also called a sine wave.
. As a result, a smooth curve that varies from +1 to -1 is formed as indicated in the blue curve below. We call this type of curves sinusoidal after the name of the sine function. This shape is also called a sine wave.
On the other hand, if you want to graph the cosine function, you need to mark the angle along the horizontal
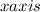 , and for each angle, you put the cosine of that angle on the vertical
, and for each angle, you put the cosine of that angle on the vertical
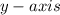 . As a result, a smooth curve that varies from +1 to -1 is formed as indicated in the red curve below. It is the same shape as the sine function but displaced to the left 90°. This is also called sinusoidal.
. As a result, a smooth curve that varies from +1 to -1 is formed as indicated in the red curve below. It is the same shape as the sine function but displaced to the left 90°. This is also called sinusoidal.
3. Maximum point
For the sine function the maximum point occurs when:
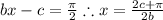
Therefore:
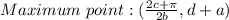
Since this is a periodic function each maximum point occurs at:

On the other hand, for the cosine function we have:
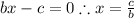
Therefore:
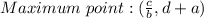
Since this is a periodic function each maximum point occurs at:
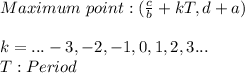
4. Minimum Point
For the sine function the minimum point occurs when:

Therefore:
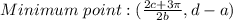
Since this is a periodic function each minimum point occurs at:
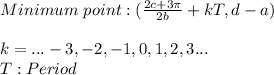
On the other hand, for the cosine function we have:
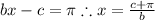
Therefore:
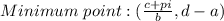
Since this is a periodic function each maximum point occurs at:
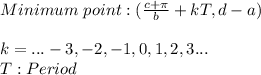
5. Domain
The domain of the sine and cosine functions is the set of all real numbers, that is:
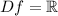
6. Range
The range of the sine and cosine function in its standard form is:
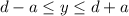
7. The x-intercept
For cosine and sine functions in its standard forms there are two possibilities:
a. The graph intersects the x-axis at infinitely many points.
b. The graph does not intersects the x-axis.
8. The y-intercept
For cosine function the y-intercept occurs at:
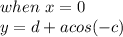
On the other hand, for sine function the y-intercept occurs at:
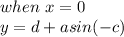
9. Phase shift
The constant
 in the equations
in the equations
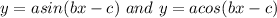
Creates a horizontal translation (shift) of the basic sine and cosine curves. So the graphs are shifted an amount
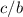 , so this number is called the phase shift.
, so this number is called the phase shift.
10. Amplitude
The amplitude of sine and cosine functions represents half the distance between the maximum and minimum values of the function and is given by:
