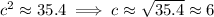1 Answer

Ubiguchi · Answer 1 · 2019-07-30T17:06:28+0000

This case can be solved via the Law of cosines, which applies exactly to this problem:

Suppose you know two sides
and
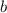of a triangle, and the angle
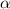$\alpha$ between them.

Then, the third side
satisfies the following equation:

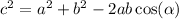
$c^2 = a^2+b^2-2ab\cos(\alpha)$

In our case, the equation becomes

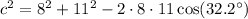
$c^2 = 8^2+11^2-2\cdot 8 \cdot 11\cos(32.2^\circ)$

We can simplify the expression:

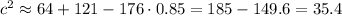
$c^2 \approx 64+121-176\cdot 0.85 = 185 - 149.6 = 35.4$

So, we have

$c^2 \approx 35.4 \implies c \approx √(35.4) \approx 6$

Please log in or register to add a comment.