The inverse of this function would be f(x) =
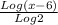 .
.
You can find the value of any inverse function by switching the f(x) and the x value. Then you can solve for the new f(x) value. The end result will be your new inverse function. The step-by-step process is below.
f(x) =
 - 6 ----> Switch f(x) and x
- 6 ----> Switch f(x) and x
x =
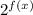 - 6 ----> Add 6 to both sides
- 6 ----> Add 6 to both sides
x + 6 =
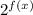 -----> Take the logarithm of both sides in order to get the f(x) out of the exponent
-----> Take the logarithm of both sides in order to get the f(x) out of the exponent
Log(x + 6) = f(x)Log2 ----> Now divide both sides by Log2
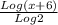 = f(x) ----> And switch the order for formatting purposes.
= f(x) ----> And switch the order for formatting purposes.
f(x) =
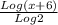
And that would be your new inverse function.