Question

In 1985, the cost of clothing for a certain family was $620. In 1995, 10 years later, the cost of clothing for this family was $1,000. Assuming the cost increased linearly, what was the cost of this family’s clothing in 1991?

Answer 1

Hi there!

The 1ˢᵗ Step is to develop a relation between cost and time (in years).

∵ th' cost increases linearly, we know that the relation can be represented by the equation of a straight line, y = mx+b

where,

• y is the cost
• m is the rate of cost increase
• x is the year
• b is the initial cost of the time frame being analyzed.

∵ We're looking at the time between 1985 and 1995 :-

The initial cost will be the cost of the clothing in 1985, which is $620.

Next, the rate of increase of the cost can be found by the rise-over-run method.

∵ y is the cost and x is the time in years, the rise will be the change in cost and the run will be the change in time (years).


`\bf {In \:other\: words}` :-


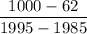
`\frac { 1000 - 62}{1995 - 1985}` = $ 37.5 per year increase

Finally, th' relation:

y = 37.5x + 620

y = 37.5 × 6 + 620

y = $ 845

Hence,
The cost of family's clothing in 1991 is $ 845.

~ Hope it helps!

Answer 2

The cost of this family’s clothing in 1991 is $ 848.

Explanation:

Given,

The cost of clothing is increasing linearly,

Let the equation that represent the cost of clothing ( in dollars ) after x years since 1985,

y = mx + c

Given, for x = 0, y = 620,

⇒ 620 = m(0) + c

⇒ c = 620,

The number of years from 1985 to 1995 = 10 years,

So, if x = 10, y = 1000,

1000 = 10(m) + c

1000 = 10m + 620

380 = 10m

⇒ m = 38,

Hence, the function that represents the cost of clothing would be,

y = 38x + 620

If x = 6,

y = 38(6) + 620 = 848

Therefore, the cost of this family’s clothing in 1991 is $ 848.