Question

. If an object travels at a constant velocity, how does its average velocity compare to its

instantaneous
velocity throughout the trip?

Answer 1

The average velocity is equal to the instantaneous velocity

Step-by-step explanation:

The average velocity,
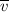`\overline v`, is given as follows;

`\overline v = (\Delta y)/(\Delta t)`

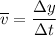
Where;

Δy = The change in displacement

Δt = The change in time

The instantaneous velocity is the derivative found of the position of the object's displacement with respect to time

Therefore, the instantaneous velocity,
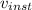`v_(inst)` = The limit of the average velocity as the change in time becomes closer to zero

`v_(inst) = \lim_(t \to 0) \left ((\Delta y)/(\Delta t) \right ) = (dy)/(dx)`

When the velocity is constant, the displacement time graph is a straight line graph, and the slope of the displacement-time graph which is the same as the velocity is constant and therefore, we have;

`Slope \ of \ straight \ line \ graph = (y_2 - y_1)/(t_2 - t_1) = (\Delta y)/(\Delta t)= (dy)/(dx)`

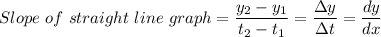
Therefore, for constant velocity, we have,
`\overline v` =
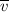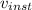`v_(inst)` the average velocity is equal to the instantaneous velocity.