Assuming each birth can give life to a boy or girl with equal chance, then the probability of having a girl is

The probability of having exactly six girls is given by Bernoulli rule:

As for the second point, let's compute the probabilty of having zero, one or two boys, which is the same of having six or more girls, but requires less calculations:
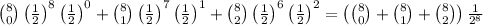
which simplifies to
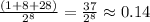
Finally, I am not sure of what you mean with the point c, so please clarify the question.