121 is big enough to assume normality and not worry about the t distribution. By the 68-95-99.7 rule a 95% confidence interval includes plus or minus two standard deviations. So 95% of the cars will be in the mph range
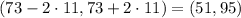
The question is a bit vague, but it seems we're being asked for the 95% confidence interval on the average of 121 cars. The 121 is a hint of course.
The standard deviation of the average is in general the standard deviation of the individual samples divided by the square root of n:

So repeating our experiment of taking the average 121 cars over and over, we expect 95% of the averages to be in the mph range
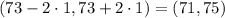
That's probably the answer they're looking for.