Answer:
The interior angles of triangle EFG are 30°, 50° and 100°.
Explanation:
We know by given that
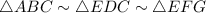 .
.
Similarities refers to proportional sides and congruent angles, so
 , by corresponding elements.
, by corresponding elements.
Therefore,
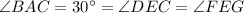
By the same reason,
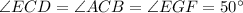
Then,
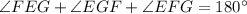 , by internal angles theorem.
, by internal angles theorem.
Replacing values, we have
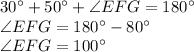
Therefore, the interior angles of triangle EFG are 30°, 50° and 100°.