Question

A line passes through (3, –2) and (6, 2). a. Write an equation for the line in point-slope form. b. Rewrite the equation in standard form using integers.

a. y+2=4/3(x-3);-4x-3y=-18

b. y-2=4/3(x-3);-4x-3y=18

c. y+2=4/3(x+3);-4x+3y=-18

d. y-3=4/3(x+2);-4x+3y=17

I need help!!!!!

Answer 1

First thing you have to do if you're going to write this line's equation in point-slope form is to find the slope. Use the points in the slope formula as follows:
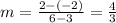`m=(2-(-2))/(6-3)=(4)/(3)`. So the slope is 4/3. The point-slope form of a line is
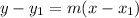`y-y_(1)=m(x-x_(1))` where x1 is the x-coordinate from either point, and y1 is the y coordinate from the SAME point as the x. I'll use (3, -2) since that's the point they used in the solutions above. x is 3 and y is -2. Filling in accordingly, we have
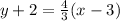`y+2=(4)/(3)(x-3)`. That is point-slope form. Now they want us to rewrite in standard form which is Ax + By = C, no fractions allowed and the x and the y have to be on the same side of the equals sign. However, before we can do that successfully, we need to rewrite the point-slope into slope-intercept. THEN we can do standard. In slope intercept, we will set the equation equal to y.
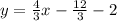`y=(4)/(3)x-(12)/(3)-2`. Simplifying a bit we get
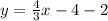`y = (4)/(3)x-4-2` or
`y=(4)/(3)x-6`. Now in order to get rid of the fraction we will multiply everything, every term, by 3. Doing that gives us
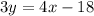`3y=4x-18`. Getting x and y on the same side is
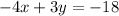`-4x+3y=-18`. I am not seeing this exact combination of point-slope and standard within the same answer. I checked my work several times, perhaps you can check how you posted the possible solutions?