So to use the elimination method, we need to put these equations on top of each other so that we can eliminate a variable:
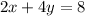
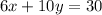
If we multiply the top equation by -3, we can eliminate the x variable:
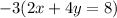
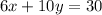
And we simplify. Then we add the two equations together:
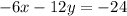
+
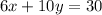
---------------------------------
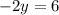
Then we solve for y:
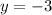
Then we need to return to one of the original equations (either will work) and plug y in. Then we will solve for x. Let's choose the first equation:
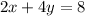
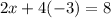
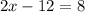
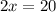
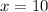
So now we know that our solution is: (10, -3).