Answer:
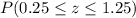
Explanation:
Consider the probability table:
z Probability
0.00 0.5000
0.25 0.59871
0.50 0.6915
0.75 0.7734
1.00 0.8413
1.25 0.8944
1.50 0.9332
1.75 0.9599
We need to find the probability which is equal to approximately 0.2957.
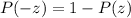
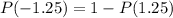
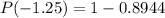
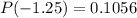
The probability of P(-1.25) is 0.1056.
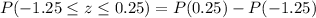

The probability of
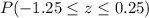 is 0.49311.
is 0.49311.

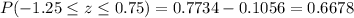
The probability of
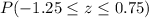 is 0.6678.
is 0.6678.
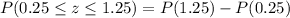
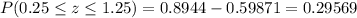
The probability of
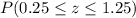 is 0.29569.
is 0.29569.
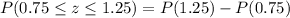
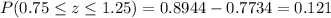
The probability of
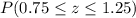 is 0.121.
is 0.121.
Therefore, the correct option is 3, i.e.,
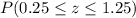 .
.