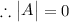Answer:
The determinant of coefficient matrix of the given system is 0.
Explanation:
Given system of equation
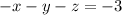
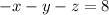
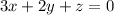
The coefficient matrix of the system
![\left[\begin{array}{ccc}-1&-1&-1\\-1&-1&-1\\3&2&1\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/vim3a73xriauwcwa9yd0hrgaccxpvodsn2.png)
Let A=
![\left[\begin{array}{ccc}-1&-1&-1\\-1&-1&-1\\3&2&1\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/vim3a73xriauwcwa9yd0hrgaccxpvodsn2.png)
X=
![\left[\begin{array}{}x&y&z\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/bhfxo0q6cr7x0aonvoavcqe342ga17sco8.png)
B=
![\left[\begin{array}-3 &8&0\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/wkn4j1q84mfwqt0kumvph6mcqw7j9op3yo.png)
Therefore , we can AX=B
![\left[\begin{array}{ccc}-1&-1&-1\\1&-1&-1\\3&2&1\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/b9q1zz34wr9ea3q020zhkhz6sf178jjumn.png)
![\left[\begin{array}{}x&y&z \end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/engfqrerg2acjqo1rtl84i823kmw7zs3qe.png) =
=
![\left[\begin{array}{}-3&8&0\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/college/m0lpgwcz9e7cy8wxhpramqw3vdu9fs6v4m.png)
The determinant of coefficient matrix of the given system is given by
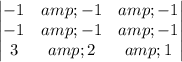
By using determinant property : when two rowsor two columns are identical then the value of determinant is equal to zero .