Question

The cost to produce a product is modeled by the function f(x) = 3x2 − 6x + 11 where x is the number of products produced. Complete the square to determine the minimum cost of producing this product.

Answer 1

Because this is a positive parabola that opens upwards, it natrually has a minimum value for the vertex. To complete the square we will first set the quadratic equal to 0 then move the constant over by subtraction. That gives us
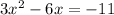`3x^2-6x=-11`. One very important rule to follow about completing the square is that the leading coefficient ALWAYS be a +1. Our is a 3. So we will factor it out like this:
`3(x^2-2x)=-11`. Next step is to take half the linear term, square it, and add it to both sides. Our linear term is 2. Half of 2 is 1, and 1 squared is 1. So we add 1 to both sides. BUT we cannot forget about that 3 we factored out. It refuses to be ignored. It is a multiplier. So when we add 1 into the set of parenthesis, we are REALLY adding in 3*1 = 3. We add 3 to the right side. All that looks like this:
`3(x^2-2x+1)=-11+3`. The right side simplifies to -8, easy enough. What we did this for, this whole entire process, was to create a perfect square binomial on the left that will serve as the x coordinate of the vertex (actually the "h" since the vertex coordinates are (h, k)). Setting up that binomial looks like this now:
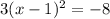`3(x-1)^2=-8`. We move the -8 back over by addition,
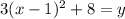`3(x-1)^2+8=y` and find that the coordinates for the vertex are (1, 8). If x (h) is 1, that is "1 product" since x is products. If y (k) is 8, that is $8. What our vertex tells us in this particular situation is that it costs $8 to make 1 item.