The optimum point occurs when supply and demand are equal.
We then have to equalize both equations:
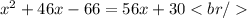
Rewriting the equation we have:
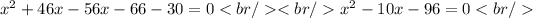
From here, we solve solve the quadratic equation and clear x:
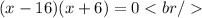
The solutions of the equation are:
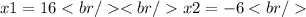
We discard the negative root.
We have then:
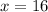
Answer:
The optimum number of items to be manufactured is:
c: 16