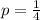Question

Assume the readings on thermometers are normally distributed with a mean of 0degreesc and a standard deviation of 1.00degreesc. find the probability that a randomly selected thermometer reads between negative 0.75 and negative 0.07 and draw a sketch of the region.

Answer 1

The thermometer nicely obeys a unit normal distribution so we just want the area under the Gaussian from
`z = -.75` to
`z=-.07`. That's a sketch of the standard bell curve with the region between -.75 and -.07 shaded in; I'll leave the actual sketching to you.

The standard normal table often only lists
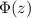`\Phi(z)`, the integral of the unit normal from negative infinity to z, for z>0. For negative z we need
`1 - \Phi(-z)`,

`p = \Phi(-.07) - \Phi(-.75) = (1- \Phi(.07)) - (1-\Phi(.75)) = \Phi(.75) - \Phi(.07)`

`\Phi(.07)=0.52790`

`\Phi(.75)=0.77337`

`p = 0.77337-0.52790=0.24547`

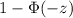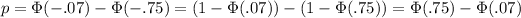
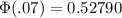
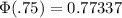
We can round that to
`p=\frac 1 4`