Question

A box is to be made from a rectangular piece of corrugated​ cardboard, where the length is 8 more inches than the​ width, by cutting a square piece 3 inches on each side from each corner and folding up the sides to form a box. the volume of the box is to be 27 cubic inches. find the dimensions of the rectangular piece of cardboard.

Answer 1

The volume of a box like this is found by multiplying the length times the width times the height. We are told that the length is 8 more inches than the width, so the width is w and the length is w + 8. If we cut away 3 square inches from each corner, the height when we fold up those corners is going to be 3. The volume is given as 27, so our formula looks like this:
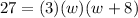
`27=(3)(w)(w+8)`. When we do that multiplication, we have
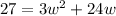
`27=3w^2+24w`. We need to solve for w so we can then solve for h. Move the 27 over and set the quadratic equal to 0.
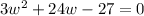
`3w^2+24w-27=0`. We can then factor out a 3 to make the job easier:
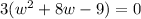
`3(w^2+8w-9)=0`. Now we can factor to solve for w. The 2 numbers that add up to 8 and multiply to -9 are 9 and -1. So (w+9) = 0, (w-1) = 0, or 3 = 0. Of course 3 doesn't equal 0, so that's out. w + 9 = 0 so w = -9. w - 1 = 0 so w = 1. There are 2 things in math that can never EVER be negative and those are time and distance/length. So -9 is out. That means that w = 1. But don't forget that there was 6 inches cut off each side, so the width is 1 + 3 + 3 which is 7. The length is w + 8 which means that the length is 7 + 8 or 15. Those are the dimensions of the rectangle before it was cut.