Question

I need help as soon as possible

Answer 1

You have 2 triangles here making up this single quadrilateral. One of the triangles is a 30-60-90 and the other one is a 45-45-90. These 2 triangles share a hypotenuse. We need the length of that hypotenuse if we are to find the missing side x. The "lower" triangle is the 30-60-90 and the side we are given is across from the 30 degree angle. In the Pythagorean triple for a 30-60-90, the side across from the 30 degree angle is x, the side across from the 60 degree angle is
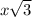
`x √(3)`, and the hypotenuse is 2x. So we need to find x. If
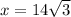
`x=14 √(3)` then two times x is equal to
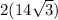
`2(14 √(3))` which is equal to
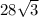
`28 √(3)`. So the length of the hypotenuse is
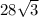
`28 √(3)`. The Pythagorean triple for a 45-45-90 is
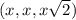
`(x,x,x √(2))` with
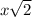
`x √(2)` as the length of the hypotenuse in a 45-45-90. If the length of the hypotenuse is
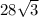
`28 √(3)`, then we need to solve for x.
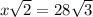
`x √(2)=28 √(3)`. We solve for x by dividing by the square root of 2, like this:
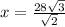
`x= (28 √(3) )/( √(2) )`. The only way to solve this is to multiply by
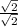
`( √(2) )/( √(2) )`. Doing this step by step we have
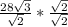
`(28 √(3) )/( √(2) )* ( √(2) )/( √(2) )`. Multiply straight across the top and straight across the bottom to get
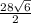
`(28 √(6) )/(2)` which simplifies by reduction to
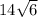
`14 √(6)`. First choice above.

Answer 2

30 60 90 triangel has special abilities. 30 degree opposite is K , 60 is

`k √(3)`
and 90 is 2K , 45 45 90 triangel is ; if 45 degree opposite is a and the other is same and the hypothenus( i dont know how 2 correct) is being

`a √(2)`