Question

Find the zeros of the polynomial function and state the multiplicity of each. f(x) = 3(x + 9)2(x - 9)3

Answer 1

There are zeros at x=-9 and x=9. Only two multiplicities (no exponent) plus or minus 9

Answer 2

`-9, -9, 9, 9, 9`

Explanation:

The given expression is

`f(x)=3(x+9)^(2) (x-9)^(3)`

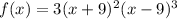
From the expression, we observe that
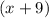`(x+9)` has a multiplicity of 2 and
`(x-9)` has a multiplicity of 3.

So, for the first factor, there's one number that makes such factor equal to zero, and that is -9, because

`x+9=0\\x=-9`

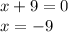
We know that this factor has a multiplicity of 2, so its zeros are -9 and -9.

We do the same process for
`(x-9)`

`x-9=0\\x=9`

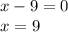
Its multiplicity is 3, so the zeros are 9, 9 and 9.

Therefore, all the zeros of the polynomial function are

`-9, -9, 9, 9, 9`