Answer:
option C
Explanation:
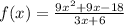
Lets factor the numerator
9x^2 +9x-18
9(x^2 +x-2)
9(x+2)(x-1)
Now we factor the denominator
3x+6
3(x+2)
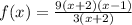
Cancel out x+2
So f(x)= 3(x-1)
now we graph f(x)
x f(x)= 3(x-1)
-2 -9
-1 -6
0 -3
1 0
We cancelled out (x+2) at the top and bottom, x+2=0 so x=-2. Hence there is a whole at x=-2
Option C represents the graph f(x) because there is a hole at (-2,-9)