Question

Find the X intercepts of a parabola with the vertex 4, -1 and a y-intercept of 0, 15

Answer 1

Let's first write this parabola's equation given the info we have. The standard form for a parabola of this type, which is a positive x^2 parabola, is
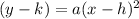
`(y-k)=a(x-h)^2`. We have the h and k as 4 and -1, respectively, and we have the x and y as 0 and 15, respectively. Filling those into formula we will solve for a:
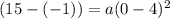
`(15-(-1))=a(0-4)^2`. This all simplifies down to a parabola with the equation
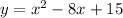
`y=x^2-8x+15`. If we factor that now we will find the x-intercepts. Set the equation equal to 0 and solve for x. The 2 numbers that add up to be a -8 and multiply to be a positive 15 are -3 and -5. So the x-intercepts of this parabola are x = -3 and x = -5.