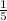Question

What is the scale factor of XYZ to UVW

Answer 1

Answer:

`\boxed {(1)/(5)}`

━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Solution-

`60 * (1)/(5) = 12`


`90 * (1)/(5) = 18`


`75 * (1)/(5) = 15`
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Hence, the answer would be
`\boxed {(1)/(5)}`

Answer 2

`(1)/(5)`

Explanation:

We want to find the scale factor of the dilation from ΔXYZ to ΔUVW.

The scale factor is given by the formula;

`k=(Image\:Length)/(Corresponding\:Object\:Length)`

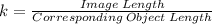
Since the dilation is from ΔXYZ to ΔUVW, our image triangle is ΔUVW.

We can now use any of the corresponding sides to determine the scale factor.

`k=(|UV|)/(|XY|)`

`\Rightarrow k=(12)/(60)`

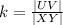
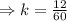
We simplify to get;

`\Rightarrow k=(12)/(12*5)`

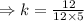
We cancel the common factors to get;

`\Rightarrow k=(1)/(5)`

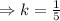
Therefore the scale factor is
`(1)/(5)`