Question

Which of the following points lies on the circle whose center is at the origin and whose radius is 5?

a) (-3, 4)
b) (1, -2)
c)

Answer 1

Let's first determine the equation for the circle in question. If the center is at the origin, then the h and k values are both 0. If the radius is 5, we can write the equation for the circle as
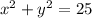
`x^2+y^2=25`. Each one of those choices for coordinates has an x and a y. We will fill in the x and y values into our equation to see if the sum of their squares is 25. Going with the first coordinate, (-3, 4), we fill in accordingly:
`(-3)^2+(4)^2=?`. -3 squared is 9 and 4 squared is 16. Does 9 + 16 = 25? Yes it does, so a. works for us. Let's try b. now, (1, -2).
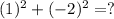
`(1)^2+(-2)^2=?`. 1 squared is 1 and -2 squared is 4. The addition of those is 5, the length of the radius. But in our standard form for a circle, the radius is a squared value, not a single value. So b. does not work. Last point of
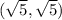
`( √(5), √(5))`. The square root of 5 squared is 5. Does 5 + 5 = 25? Of course it doesn't. The only point that is on the circle is choice a., (-3, 4).