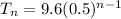Answer:
Recursive formula will be
Explanation:
The given sequence is 9.6, -4.8, 2.4, -1.2, 0.6......
In this sequence we find that there is a common ratio which makes this sequence a geometric sequence.
For a geometric sequence explicit formula is given by
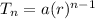 if n > 1
if n > 1
So by putting values of a = 9.6
and common ratio r =
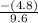 =
=
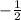
Therefore, the recursive formula will be