Question

Can someone help me with this ASAP!

Answer 1

So the equation for the volume of the sphere is
`V= (4)/(3) \pi r^3` .

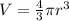
For this, you'll need to plug in 128 pi into the volume placeholder and solve for r.


`128 \pi = (4)/(3) \pi r^3`

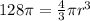
Firstly, divide by pi on each side of the equation to cancel out pi. Your equation will look like this:
`128=(4)/(3)r^3`

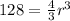
Next, you'll want to multiply 3/4 on each side to cancel out 4/3. Your equation will look like this:
`96=r^3`

Lastly, you'll want to 3rd root each side of the equation, and your answer should be
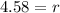
`4.58=r` . The correct option is B. 4.58