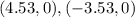Question

Find the x-intercepts of the parabola with vertex (1,-17) and y-intercept (0,-16)...

Write your answer in (x1,y1) , (x2,y2).

Answer 1

To solve this problem you must apply the proccedure shown below:

1. You have that the standard form of the equation for a parabola is:

`y=a(x-h)^(2)+k`

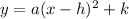
Where
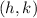`(h,k)` is the vertex

2. Substitute the values shown into the equation:

`y=a(x-1)^(2) -17`

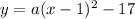
3. Now, substitute
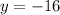`y=-16` and
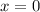`x=0` to calculate
`a`:

`-16=a(0-1)^(2) -17\\ a=1`

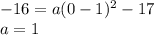
4. Then, the equation of the parabola is:

`y=(x-1)^(2) -17`

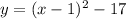
5. To calculate the x-intecept
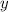`y` must be
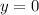`y=0`. Substitute it into the equation and solve for
`x`:

`image`

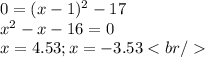
The answer is:
`(4.53,0),(-3.53,0)`