Question

What is the length of the segment whose endpoints are A(-4, 3) and B (10, 6)?

3sqrt5

sqrt205

sqrt93

3sqrt6

Answer 1

Apply Pythagoras:

length = sqrt( (10--4)² + (6-3)² ) = sqrt(205)

Answer 2

Answer: The correct option is (B)
`√(205).`

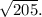
Step-by-step explanation: We are given to find the length of the segment whose endpoints are A(-4, 3) and B (10, 6).

We know that

the length of a line segment with endpoints (a, b) and (c, d) is calculated using distance formula as follows :

`D=√((c-a)^2+(d-b)^2).`

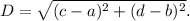
Therefore, using distance formula, the distance between the endpoints A(-4, 3) and B (10, 6) is given by

`AB\\\\=√((10-(-4))^2+(6-3)^2)\\\\=√((10+4)^2+3^2)\\\\=√(14^2+9)\\\\=√(196+9)\\\\=√(205).`

Thus, the length of the line segment AB is
`√(205)~\textup{units}.`

Option (B) is CORRECT.