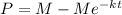Question

In a previous exercise we formulated a model for learning in the form of the differential equation dp dt = k(m − p) where p(t) measures the performance of someone learning a skill after a training time t, m is the maximum level of performance, and k is a positive constant. solve this differential equation to find an expression for p(t). (use p for p(t). assume that p(0) = 0.) incorrect: your answer is incorrect.

Answer 1

Hi there!


`(dP)/(dt) = k(M-P)`

⇒
`(dP)/(M-P) = k`


`\textbf{Integrate\: both \:sides\: of\: th'\: Eqn.}` :-


`\int (dP)/(M-P) = \int kdt`

⇒
`\ln|M-P| = kt + C`

⇒
`\ln|M-P| = -kt - C`

Since,

`u = M - P \implies du = -1dP \implies dP = -du`

∴
`\int (dP)/(M-P) \\e \ln|M - P|`


:-


`\ln|M-P| = -kt - C`

⇒
`|M - P| = e^(-kt - C)`

⇒
`M - P = \pm e^(-kt - C)`


`\textbf{Further solving}` :-

⇒
`M - P = \pm e^(-kt - C)`

⇒
`M - P = \pm e^(- C - kt)`

⇒
`M - P = \pm e^(- C + (- kt))`

⇒
`M - P = \pm e^(- C) × e^(- kt)`

⇒
`M - P = Ke^(- kt)`

⇒
`M = Ke^(- kt) + P`

⇒
`P = M - Ke^(- kt)`


`\textbf{Let \:P(0) \:= \:0, \:then \:set\: t\: =\: 0\: and\: P \:= \:0}` :-


`0 = M - Ke^(- k × 0)`

⇒
`0 = M - K × 1`

⇒
`M = K`

Substitute th' following value in Original Eq :-


`\boxed{P = M - Me^(-kt)}`


~ Hope it helps!

Answer 2

I assume you mean


`(dP)/(dt) = k(M-P)`

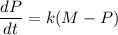ANSWER
An expression for P(t) is


`P = M - Me^(-kt)`

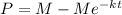
Step-by-step explanation
This is a separable differential equation. Treat M and k as constants. Then we can divide both sides by M - P to get the P term with the differential dP and multiply both sides by dt to separate dt from the P terms


`\begin{aligned} (dP)/(dt) &= k(M-P) \\ (dP)/(M-P) &= k\, dt \end{aligned}`

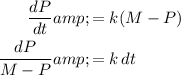Integrate both sides of the equation.


`\begin{aligned} \int (dP)/(M-P) &= \int k\, dt \\ -\ln|M-P| &= kt + C \\ \ln|M-P| &= -kt - C\end{aligned}`

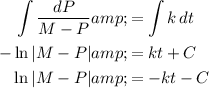
Note that for the left-hand side, u-substitution gives us


`u = M - P \implies du = -1dP \implies dP = -du`

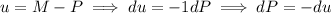
hence why
`\int (dP)/(M-P) \\e \ln|M - P|`

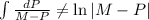
Now we use the definition of the logarithm to convert into exponential form.

The definition is


`\ln(a) = b \iff \log_e(a) = b \iff e^b = a`

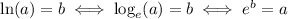
so applying it here, we get


`\begin{aligned} \ln|M-P| &= -kt - C \\ |M - P| &= e^(-kt - C) \\ M - P &= \pm e^(-kt - C) \end{aligned}`

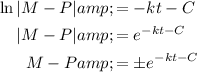
Exponent properties can be used to address the constant C. We use
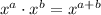
`x^(a) \cdot x^(b) = x^(a+b)` here:


`\begin{aligned} M - P &= \pm e^(-kt - C) \\ M - P &= \pm e^(- C - kt) \\ M - P &= \pm e^(- C + (- kt)) \\ M - P &= \pm e^(- C) \cdot e^(- kt) \\ M - P &= Ke^(- kt) && (\text{\footnotesize Let $K = \pm e^(-kt)$ }) \\ M &= Ke^(- kt) + P\\ P &= M - Ke^(- kt) \end{aligned}`

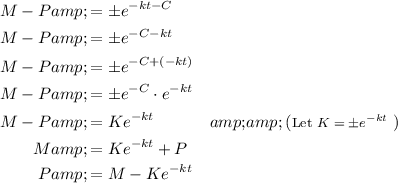
If we assume that P(0) = 0, then set t = 0 and P = 0


`\begin{aligned} 0 &= M - Ke^(- k\cdot 0) \\ 0 &= M - K \cdot 1 \\ M &= K \end{aligned}`

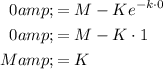
Substituting into our original equation, we get our final answer of


`P = M - Me^(-kt)`