To solve this problem you must apply the proccedure shown below:
1. The formulas for calculate the volume of a cylinder and and the volume of a sphere, are:
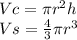
Where
 is the radius and
is the radius and
 is the height.
is the height.
2. You have that the sphere and the cylinder have the same radius and height. By definition, the height of the sphere is twice its radius. Therefore, the height of the cylinder is:
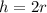
3. Substitute it into the formula for calculate the volume of a cylinder:
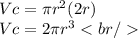
4. Now, solve for
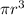 and substitute it into the formula for calculate the volume of a sphere:
and substitute it into the formula for calculate the volume of a sphere:
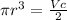
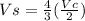
5. Now, calculate the volume of the sphere:

The answer is:
