Question

Find the correct sum of each geometric sequence.

a1 = 3, a8 = 384, r = 2
a1 = 343, an = -1, r = -1/7
a1 = 625, n= 5, r = 3/5
a1 = 4, n = 5, r = -3
a1 = 2401, n = 5, r = -1/7

Answer 1

A geometric sequence with first term "a" and common ratio "r" has "nth" term:

ar^(n-1)

And the sum of a geometric sequence with "n" terms, first term "a," and common ratio "r" has the sum "a(r^n - 1)/r - 1.

1.) 765

2.) 300

3.) 1441

4.) 244

5.) 2101

Answer 2

1.765

2.301

3.1441

4.183

5.2101

Explanation:

We are given that

1.
`a_1=3, a_8=384,r=2`

We know that sum of nth term in G.P is given by

`S_n=(a(r^n-1))/(r-1)` when r > 1

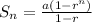`S_n=(a(1-r^n))/(1-r)` when r < 1

n=8, r=2 a=3

Therefore,
`S_8=(3((2)^8-1))/(2-1)` because r > 1

`S_8=3* (256-1)=765`

1. Sum of given G.P is 765

2.
`a_1=343,a_n=-1,r=-(1)/(7)`

nth term of G.P is given by the formula

`a_n=ar^(n-1)`

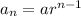
Therefore , applying the formula

`-1=343* ((-1)/(7)}^(n-1)`

`(-1)/(343)=((-1)/(7))^(n-1)`

`((-1)/(7))^3=((-1)/(7))^(n-1)`

When base equal on both side then power should be equal

Then we get n-1=3

n=3+1=4

Applying the formula of sum of G.P

`S_4=(343(1-((-1)/(7))^4))/(1-(-1)/(7))` where r < 1

`S_4=(343(1+(1)/(343)))/((8)/(7))`

`S_4=343*(344)/(343)*(7)/(8)`

`S_4=301`

3.
`a_1=625, n=5,r=(3)/(5) < 1`

Therefore,
`S_5=(625(1-((3)/(5))^5))/(1-(3)/(5))`

`S_5=625* (3125-243)/(3125)* (5)/(2)`

`S_5=625*(2882)/(3125)*(5)/(2)`

`S_5=1441`

4.
`a_1=4,n=5,r=-3`

`S_5=(4(1-(-3)^5)/(1-(-3))` where r < 1

`S_5=(3(1+243))/(1+3)`

`S_5=3* 61=183`

5.
`a_1=2402,n=5,r=(-1)/(7)`

`S_5=(2401(1-((-1)/(7))^5))/(1-(-1)/(7))` r < 1

`S_5=(2401(1+(1)/(16807)))/((7+1)/(7))`

`S_5=2401*(16808)/(16807)*(7)/(8)`

`S_5=2101`