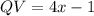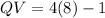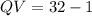Answer
The length of QV is 31 units
Explanation
Notice that triangle STR and triangle TQR are congruent by Side-Angle-Side, so ST = TQ
We also know that TQ = 26, and we can infer from our diagram that
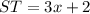 , so let's replace the values:
, so let's replace the values:
ST = TQ
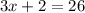
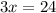
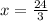
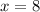
Also, notice that triangle SVR is congruent to Triangle VQR by Side-Angle-Side as well, so QV = SV
We know that
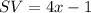 , so let's replace the value:
, so let's replace the value:
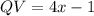
Since we know that
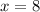 , we can replace the value to find QV:
, we can replace the value to find QV: