Answer:
k = 0.209
Explanation:
The given expression in the question is C =
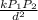
Where
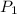 and
and
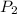 are the populations of the two cities and d is the distance between the cities.
are the populations of the two cities and d is the distance between the cities.
If the distance between the cities d is 480 miles
Population of the cities are
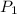 = 95000 and
= 95000 and
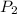 =2900000 respectively.
=2900000 respectively.
And average number of the daily phone calls is 250000.
Then we have to find the value of k.
C =
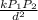
250000 =
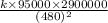
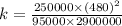
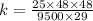
k = 0.2091 ≈ 0.209
k = 0.209 is the answer.