Starting with 3 and working our way up, we last have 3 people left. Before that, half of the remaining audience has left. That means that if the amount of people remaining during those twenty more minutes is represented by the variable a, this means that 1/2 of a has left, leaving us with 1a-(1/2)a=(1/2)a using the distributive property. Thus, if (1/2)a=3, we multiply both sides by 2 to get 6 people. Before those twenty minutes, a third of the audience left. Therefore, if we assign the variable b to the amount of people in the audience during those 10 minutes, we have b-(1/3)b=1b-(1/3)b=b(1-1/3)=(2/3)b as the amount of people after a third of the audience leaves, or a (6). Therefore, since (2/3)b=6, we can multiply both sides by 3 to get 2b=18. Next, we can divide both sides by 2 to get b=9. There's only one step left at this point, and it's half of the students leaving - using something similar from what we used to get 3 to 6 in our first step, we have 9*2=18 as our starting audience.
The following text is an alternate way to solve the problem.
Assigning the starting number of students to the variable x, we first see that one half, or 1/2, students leave after 5 minutes. This means that we are currently at (1/2)x, or x/2 by multiplying the numerator (1) by x. We get (1/2)x because we started with x, and (1/2)x , or 0.5x, leaves, so 1x-0.5x=x(1-0.5) using the distributive property. Next, 10 minutes later, a third of the current audience leaves. This means that a third of (1/2)x leaves, so we can figure out 1/3 of (1/2)x by multiplying that by 1/3, leaving us with
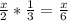
. We then subtract that from (1/2)x (which is equal to 3x/6 by multiplying the fraction by 3/3, or 1, using the identity property), leaving us with (3/6)x-(2/6)x=x/6. Next, after 20 minutes, half of the remaining audience leaves, so we have 1/2 of (x/6) left. Multiplying the two together, we have x/12=3. Multiplying both sides by 12, we get x=36.
Feel free to ask further questions!