Question

What are the period and phase shift for f(x) = −4 tan(x − π)?

Answer 1

The general form for the tangent equation is y = (a)tan(bx-c)+d where a is the amplitude, b is the period and c is the phase shift. The period of the tangent graph is pi, and the formula to solve for the period is then
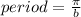
`period= ( \pi )/(b)`. Our b value is 1, so the period of this tangent curve is pi. The formula for the phase shift is
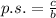
`p.s.= (c)/(b)` and for us that is pi/1. So the period for this curve is pi, and the phase shift is pi units to the right.

Answer 2

`\bf ~~~~~~~~~~~~\textit{function transformations} \\\\\\ % function transformations for trigonometric functions % templates f(x)=Asin(Bx+C)+D \\\\ f(x)=Acos(Bx+C)+D\\\\ f(x)=Atan(Bx+C)+D \\\\ -------------------`


`\bf \bullet \textit{ stretches or shrinks}\\ ~~~~~~\textit{horizontally by amplitude } A\cdot B\\\\ \bullet \textit{ flips it upside-down if }A\textit{ is negative}\\ ~~~~~~\textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if }B\textit{ is negative}`


`\bf ~~~~~~\textit{reflection over the y-axis} \\\\ \bullet \textit{ horizontal shift by }(C)/(B)\\ ~~~~~~if\ (C)/(B)\textit{ is negative, to the right}\\\\ ~~~~~~if\ (C)/(B)\textit{ is positive, to the left}\\\\ \bullet \textit{vertical shift by }D\\ ~~~~~~if\ D\textit{ is negative, downwards}\\\\ ~~~~~~if\ D\textit{ is positive, upwards}`


`\bf \bullet \textit{function period or frequency}\\ ~~~~~~(2\pi )/(B)\ for\ cos(\theta),\ sin(\theta),\ sec(\theta),\ csc(\theta)\\\\ ~~~~~~(\pi )/(B)\ for\ tan(\theta),\ cot(\theta)`

with that template in mind, let's see this one.


`\bf f(x)=\stackrel{A}{-4}tan(\stackrel{B}{1}x\stackrel{C}{-\pi })+\stackrel{D}{0} \\\\\\ \stackrel{period}{\cfrac{2\pi }{B}\implies \cfrac{2\pi }{1}\implies 2\pi } \\\\\\ \stackrel{phase/horizontal~shift}{\cfrac{C}{B}\implies \cfrac{-\pi }{1}}\implies -\pi \qquad \textit{shifted to the right by }\pi \textit{ units}`