To find the length of the sides, we use the Pythagorean Theorem. First, let's look at the side RS. R is at (1,3), and S is at (3,1). Therefore, to find RS, we use the difference in height and length:
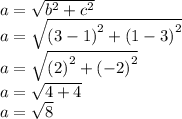
The length of side RS is square root 8.
Side ST is made from point S (3,1) and point T (5,2).
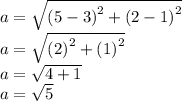
The length of side ST is root 5.
Side RT is between R (1,3) and T (5,2).

The side RT is root 17. The triangle is scalene, meaning it has three sides of different lengths.