Question

If Julie invests $9,250 at a rate of 7%, compounded weekly, find the value of the investment after 5 years. $13,455.78 $12,487.50 $32,370.50 $13,123.29

Answer 1

$13,123.29

Explanation:

Answer 2

The formula we need here is
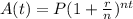
`A(t)=P(1+ (r)/(n)) ^(nt)`, where A(t) is the amount at the end of it all, P is the initial investment, n is the number of times the money is compounded (I'll explain in a sec), and t is the time we invest our money in years. Going back to n, if the money is invested for 1 year, n = 1 because it is compounded once; if the money is invested for 6 months, n = 2 (twice a year the money is compounded), if n = 4, the money is compounded quarterly; if n = 52, the money is compounded weekly. See? For us, the equation is filled in with these values: P = 9250, r = 7% or .07, t = 5, n = 52.
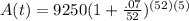
`A(t)=9250(1+ (.07)/(52))^{(52)(5)` which simplifies a bit to
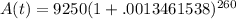
`A(t)=9250(1+.0013461538)^(260)`. Doing the adding inside the parenthesis we have
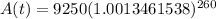
`A(t)=9250(1.0013461538)^(260)`. Raise the parenthesis value to the exponent of 260 to get A(t)=9250(1.418733571) . Now we can find the amount we will have after 5 years of "growing" $9,250 that's compounded weekly at a rate of 7%. A(t) = $13,123.2, last choice above.