Answer: the correct option is (B) Positive.
Step-by-step explanation: We are given to select the correct option about the discriminant of the graphed function.
We see that
the graph shows a quadratic function, since there are two ends and both goes on the same side.
We know that
for a function
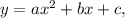 the discriminant is given by
the discriminant is given by
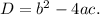
Also,
the quadratic equation will have
(i) one real root if D = 0,
(ii) two real roots if D > 0,
(iii) two unreal roots if D < 0.
From the graph, we see that there are two solutions of f(x) = 0. These are
x = -3 and x = -1.5.
Therefore, the given function will have two real roots. This implies that the discriminant of the graphed function is positive.
Option (B) is CORRECT.