Part A:
For a table to be considered a function, every x-value must have one y-value.
Each x-value in this table is unique, and has only one y-value, so this table
does represent a function.Part B:
Plug in 7 for every x in the relation:
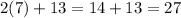
The table's output when x = 7 is 11. Compare the two outputs:
11 < 27
The relation, 2x + 13, has a greater value when x = 7.
Part C:
Set the relation to equal 75:
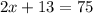
Subtract 13 from both sides:

Divide both sides by 2 to get x by itself:
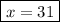
The x value that produces an output of 75 will be
31.