Question

Which two values of x are roots of the polynomial below? x2 + 3x + 5

Answer 1

Your polynomial is a quadratic, a second degree polynomial, to be exact. It can be factored to solve for those values of x you are looking for. Depending upon how you're factoring in class, solving can be done 1 of several ways but the never-fail way is the quadratic formula. Putting those values into the quadratic formula gives us this:
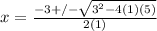
`x= (-3+/- √(3^2-4(1)(5)) )/(2(1))` which simplifies to
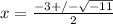
`x= (-3+/- √(-11) )/(2)`. We have to deal with the square root of -11 now. Rewriting using the imaginary i gives us
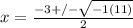
`x= (-3+/- √(-1(11)) )/(2)`. Since -1 is equal to i^2, we can make that replacement in our formula:
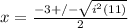
`x= (-3+/- √(i^2(11)) )/(2)`. We can now pull out a single i from the i^2 and write the answer in standard form.
`x= (-3+/-i √(11) )/(2)`.
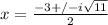
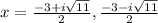
`x= (-3+i √(11) )/(2) , (-3-i √(11) )/(2)`. Standard form is
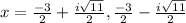
`x= (-3)/(2)+ (i √(11) )/(2), (-3)/(2)- (i √(11) )/(2)`. There you go!