Question

For what values of x is the expression below defined?

Answer 1

A) -5
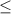`\leq` x < 1

Explanation:

First, let's notice that we need positives numbers inside both roots. The root of a negative number is a math error (we are not dealing with complex numbers right now). With that information, let's analyze the options:

A) -5
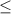`\leq` x < 1

If we add 5 in this inequation, we have

-5+ 5
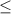`\leq` x+5 < 1+5

0
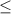`\leq` x+5 < 6

That's means the number in the first root is positive, great!

Now, we want 1-x to be positive:

-5
`\leq` x < 1

5
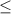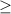`\geq` -x > -1 (remember that the inequation changes side when we multiply by a negative number, (-1) in this case)

1+5
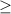`\geq` 1-x > 1-1

6
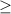`\geq` 1-x > 0

It's positive!

This is the correct answer but let's see why the others are incorrect.

B)5> x
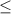`\leq`-1

We just need to find a number that fits the inequation but causes at least one root to have a negative number inside.

For example, -6.

5>-6

-6
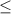`\leq` -1

But -6+5 = -1 is negative

C) 5 > x > 1

In this case, the number 2 fits the inequation but it causes the second root to have a negative number inside, 1 - 2 = -1

D) 5
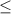`\leq` x
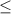`\leq` 1

This option can't be correct because there is no number smaller than 1 and bigger than 5.